第一讲 基础算法

1. 前缀和

二维前缀和就是可以O（1）时间内求出任意两点组成的矩形的所有元素的和

acwing 796. 子矩阵的和 https://www.acwing.com/problem/content/description/798/

import java.util.*;

class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt(), m = sc.nextInt(), q = sc.nextInt();
        int[][] arr = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                arr[i][j] = sc.nextInt();
            }
        }
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                arr[i][j] += arr[i - 1][j] + arr[i][j - 1] - arr[i - 1][j - 1];
            }
        }
        
        for (int i = 0; i < q; i++) {
            int x1 = sc.nextInt(), y1 = sc.nextInt(), x2 = sc.nextInt(), y2 = sc.nextInt();
            System.out.println(arr[x2][y2] - arr[x2][y1 - 1] - arr[x1 - 1][y2] + arr[x1 - 1][y1 - 1]);
        }
        
        sc.close();
    }
}

2. 差分

差分：需要构建一个数组，使得新数组的前缀和数组为原数组

这样就能在O(1)时间内完成某个区间的每个元素都加上C（通过差分数组的两端点：+C和-C）

acwing 797. 差分 https://www.acwing.com/problem/content/799/

import java.util.*;

class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt(), m = sc.nextInt();
        int[] arr = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            arr[i] = sc.nextInt();
        }
        int[] dif = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            dif[i] = arr[i] - arr[i - 1]; 
        }
        
        for (int i = 0; i < m; i++) {
            int L = sc.nextInt(), R = sc.nextInt(), C = sc.nextInt();
            dif[L] += C;
            if (R + 1 <= n)
                dif[R + 1] -= C;
        }
        
        for (int i = 1; i <= n; i++) {
            dif[i] += dif[i - 1];
        }
        //输出
        
        for (int i = 1; i <= n; i++) {
            System.out.print(dif[i] + " ");
        }
        
        sc.close();
    }
}

二维差分：

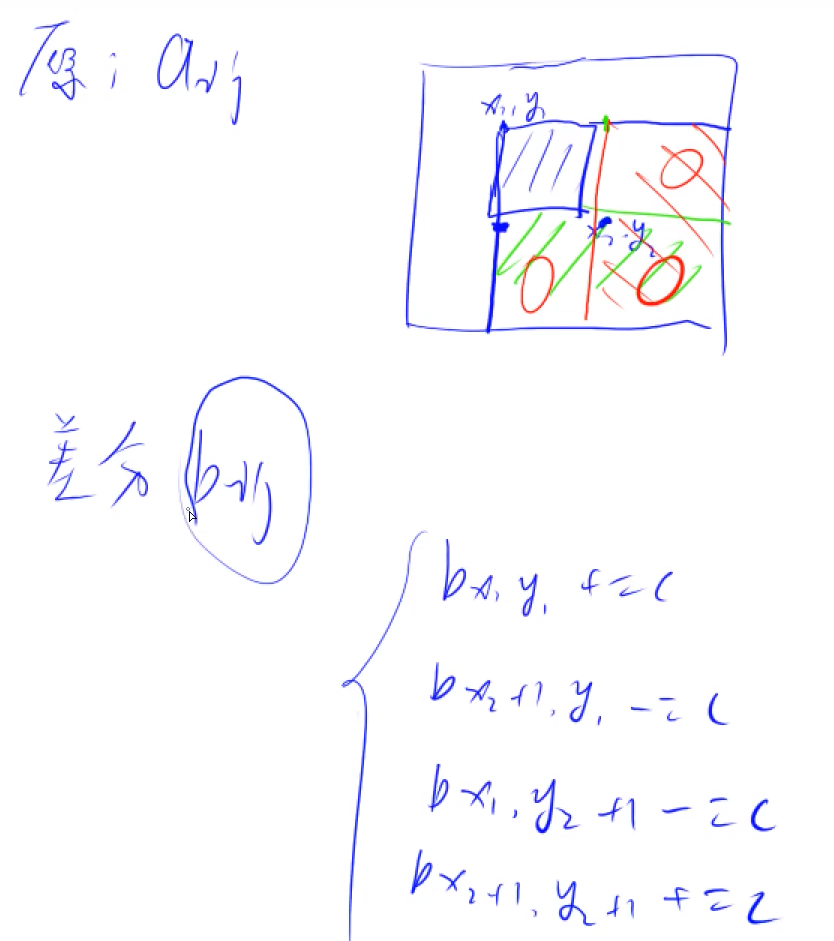
acwing 798. 差分矩阵 https://www.acwing.com/problem/content/800/

import java.util.*;

class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt(), m = sc.nextInt(), q = sc.nextInt();
        int[][] arr = new int[n + 1][m + 1];
        int[][] dif = new int[n + 1][m + 1];
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                arr[i][j] = sc.nextInt();
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                dif[i + 1][j + 1] = arr[i + 1][j + 1] - arr[i + 1][j] - arr[i][j + 1] + arr[i][j];
            }
        }
        
        for (int i = 0; i < q; i++) {
            int x1 = sc.nextInt(), y1 = sc.nextInt(), x2 = sc.nextInt(), y2 = sc.nextInt(), c = sc.nextInt();
            dif[x1][y1] += c;
            if (x2 + 1 <= n)
                dif[x2 + 1][y1] -= c;
            if (y2 + 1 <= m)
                dif[x1][y2 + 1] -= c;
            if (x2 + 1 <= n && y2 + 1 <= m)
                dif[x2 + 1][y2 + 1] += c;
        }
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dif[i][j] += dif[i][j - 1] + dif[i - 1][j] - dif[i - 1][j - 1];
            }
        }
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                System.out.print(dif[i][j] + " ");
            }
            System.out.println();
        }
        
        sc.close();
    }
}

3. 离散化

由于数据范围太大（如果为了O（1）访问，直接开大数组会内存溢出），因此将这些数通过排序映射到0, 1 , 2, 3... n，这样就能用O(logN)的时间得到原数的映射（即下标）

类似于哈希

acwing 802. 区间和 https://www.acwing.com/problem/content/804/

import java.util.*;

class Main {
    static class Pair {
        int L;
        int R;
        Pair(int L, int R) {
            this.L = L;
            this.R = R;
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt(), m = sc.nextInt();
        List<Pair> adds = new ArrayList<>();
        List<Pair> qureys = new ArrayList<>();
        Set<Integer> idxSet = new HashSet<>();
        
        for (int i = 0; i < n; i++) {
            int x = sc.nextInt(), c = sc.nextInt();
            adds.add(new Pair(x, c));
            idxSet.add(x);
        }
        for (int i = 0; i < m; i++) {
            int l = sc.nextInt(), r = sc.nextInt();
            idxSet.add(l);
            idxSet.add(r);
            qureys.add(new Pair(l, r));
        }
        List<Integer> idxs = new ArrayList<>(idxSet);
        Collections.sort(idxs);
        
        int N = idxs.size(); 
        int[] arr = new int[N + 1];
        for (Pair add : adds) {
            arr[find(idxs, add.L)] += add.R;
        }
        for (int i = 1; i <= N; i++) {
            arr[i] += arr[i - 1];
        }
        for (Pair qurey : qureys) {
            System.out.println(arr[find(idxs, qurey.R)] - arr[find(idxs, qurey.L) - 1]);
        }
        
        sc.close();
    }
    
    public static int find(List<Integer> list, int x) {
        int L = 0, R = list.size() - 1;
        while (L <= R) {
            int mid = L + (R - L) / 2;
            if (list.get(mid) < x) {
                L = mid + 1;
            } else if (list.get(mid) > x) {
                R = mid - 1;
            } else {
                return mid + 1;
            }
        }
        return 0;
    }
    
}